¿Pueden imaginar el recorrido de los fotones en la nebulosa del cangrejo?
Lo mismo que las imágenes de la nebulosa del cangrejo, la imagen de la izquierda bien podría ser utilizada como resumen de lo visto hasta ahora en el curso.
domingo, 27 de septiembre de 2009
Resumen gráfico. A propósito de la primera evaluación.
¿Pueden imaginar el recorrido de los fotones en la nebulosa del cangrejo?
domingo, 20 de septiembre de 2009
El brillo de las estrellas.
Filtros
Las magnitudes aparentes de las estrellas se miden utilizando filtros.
Checa el vínculo a un simulador de filtros...
http://astro.unl.edu/naap/blackbody/blackbody.html
Ahora que sabemos cómo determinar la distancia a estrellas próximas, podemos medir su luminosidad, lo que nos permitirá cuantificar cuánta energía en forma de radiación sale de la estrella por segundo en todas direcciones. Sin embargo, primeramente debemos familiarizarnos con el método de medición del brillo estelar.
Al término de esta unidad, debemos distinguir entre dos ideas: el brillo aparente, que se refiere al brillo con que percibimos a una estrella sin tomar en cuenta la distancia a la que se encuentra, y el brillo intrínseco o absoluto, que se refiere a la manera en que percibiríamos a una estrella si se ubicara a una distancia estándar.
Brillo aparente y el concepto de Magnitud.
El brillo aparente es una medida, en alguna escala acptable de la cantidad de energía radiante por segundo de la estrella que llega a un centímetro cuatrado de una superficie sensible (la retina del ojo, una detector astronómico, etc.). La escala que utilizamos para medir el brillo aparente de las estrellas no se basa en una unidad de energía como el ergio, sino en un sistema en el cual ciertas estrellas son tomadas como estándares. En otras palabras, introducimos una escala en la cual todas las estrellas son comparadas con ciertas estrellas estándares.
¿Sabes cuál es el criterio para la elección de estas estándares? ¿Conoces el nombre de alguna estrella estándar?
Al término de esta unidad, debemos distinguir entre dos ideas: el brillo aparente, que se refiere al brillo con que percibimos a una estrella sin tomar en cuenta la distancia a la que se encuentra, y el brillo intrínseco o absoluto, que se refiere a la manera en que percibiríamos a una estrella si se ubicara a una distancia estándar.
Brillo aparente y el concepto de Magnitud.
El brillo aparente es una medida, en alguna escala acptable de la cantidad de energía radiante por segundo de la estrella que llega a un centímetro cuatrado de una superficie sensible (la retina del ojo, una detector astronómico, etc.). La escala que utilizamos para medir el brillo aparente de las estrellas no se basa en una unidad de energía como el ergio, sino en un sistema en el cual ciertas estrellas son tomadas como estándares. En otras palabras, introducimos una escala en la cual todas las estrellas son comparadas con ciertas estrellas estándares.
¿Sabes cuál es el criterio para la elección de estas estándares? ¿Conoces el nombre de alguna estrella estándar?
jueves, 17 de septiembre de 2009
Buena página de astrofotografía...
Para quienes estén interesados, yo creo que la astrofotografía es un excelente pretexto para iniciar un club... chequen...
http://www.astrolleida.net/esp/indexesp.htm
http://www.astrolleida.net/esp/indexesp.htm
miércoles, 9 de septiembre de 2009
¿Por qué el cielo es azul?
Imagen: http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html
La difusión de la luz por parte de la atmósfera tiene además un efecto extraordinario y de gran importancia: el azul del cielo. El espacio cósmico es de por sí oscuro. Los astronautas en órbita fuera de la atmósfera ven al mismo tiempo el Sol y miríadas de estrellas sobre un cielo completamente negro.
En cambio, en los rayos que inciden en el ojo directamente desde el Sol, es menor el porcentaje de luz azul y se verifica por lo tanto un enrojecimiento. El fenómeno se acentúa marcadamente cuando el Sol u otro astro está muy bajo sobre el horizonte (porque la luz tiene que atravesar una cantidad de aire bastante mayor), lo cual explica el color rojizo del Sol cuando acaba de salir o cuando está próximo a ponerse.
El azul del cielo
Cuando la luz solar penetra en la atmósfera, no todos sus fotones prosiguen su trayectoria en línea recta: una parte, como ya sabemos, se dispersa en todas direcciones al chocar contra las moléculas. Después de sufrir numerosísimas colisiones, estos fotones dispersados llegan al ojo del observador desde todas las direcciones posibles, como luz difusa. El porcentaje de luz difusa crece rápidamente con la disminución de la longitud de onda y, por este motivo, la luz azul se difunde en un porcentaje bastante maor que la luz roja; por este motivo, la luz solar que no nos llega directamente del Sol, sino de todas las direcciones del cielo, es predominantemente azul, el color característico del cielo sereno.
En cambio, en los rayos que inciden en el ojo directamente desde el Sol, es menor el porcentaje de luz azul y se verifica por lo tanto un enrojecimiento. El fenómeno se acentúa marcadamente cuando el Sol u otro astro está muy bajo sobre el horizonte (porque la luz tiene que atravesar una cantidad de aire bastante mayor), lo cual explica el color rojizo del Sol cuando acaba de salir o cuando está próximo a ponerse.
¿Afecta la atmósfera a la Astronomía?
Para los que hoy no llegaron... chequen esta info a manera de resumen, está tomada del blog de Alex Fernández, http://www.jandrochan.com/ , si les interesa saber sobre astrofotografía vale la pena visitarlo... También chequen la versión actualizada del ppt del tema en eminus.
Les recuerdo que he actualizado la lista de referencias en eminus...
¡Saludos!
El envoltorio gaseoso que rodea nuestro planeta atenúa la luz de las estrellas y confiere al cielo su color azul.
El envoltorio gaseoso que rodea nuestro planeta atenúa la luz de las estrellas y confiere al cielo su color azul.
La atmósfera que rodea la Tierra se extiende con densidad decreciente hasta cientos de kilómetros de la superficie.
Al nivel del mar, la densidad es de 1,293 kg/m^3, lo cual significa que el aire contenido en un metro cúbico (a la temperatura de 0º C) tiene una masa de 1,293 kg.
La densidad desciende hasta 0,4 kg/m^3 a 10 km de altitud, a 1,2 g/m^3 a 50 km y a tan sólo una cienmilmillonésima de gramo por metro cúbico a 300 km. Es fácil comprender entonces que los satélites artificiales encuentren una resistencia extremadamente débil por parte de la atmósfera.
La baja atmósfera (la llamada troposfera, por debajo de los 12 km) está constituida esencialmente por nitrógeno, oxígeno y argón, presentes en proporciones constantes (75,5%, 23,2% y 1,3% respectivamente, en peso). Además de indicios de otros gases, hay en el aire pequeñas cantidades variables de dióxido de carbono y de vapor de agua. Este último, con su proporción variable (2% como máximo), determina el grado de humedad del aire.
Entre 20 y 40 km de altitud, es decir, en la región superior de la estratosfera (estrato atmosférico situado por encima de la troposfera), se encuentra el ozono (molécula formada por tres átomos de oxígeno), que aunque está presente en pequeñas concentraciones (alrededor del 1%), el ozono absorbe completamente la radiación ultravioleta del Sol de la ongitud de onda inferior a 0,3 μm e impide que llegue al suelo. Si esta radiación no fuera absorbida por el ozono, la vida en la Tierra sería muy difícil por no decir imposible.
domingo, 6 de septiembre de 2009
Astronomía y Astrofísica
Les debía esta entrada... además de este vínculo a Astronomy notes, nos sirvieron de referencia para iniciar el curso y pueden ser de utilidad para ustedes...
http://www.astronomynotes.com/chapter1/s3.htm
Astronomía y Astrofísica.
Desde tiempos inmemoriales, el hombre se ha ocupado de la contemplación del cielo nocturno. Sabemos de esto gracias al estudio de un gran número de elementos (pinturas rupestres, estelas, códices, escritos, grabados, catálogos, etc.) en los que nuestros antepasados registraron sus conocimientos y que han llegado hasta nuestros días. De entre estos elementos, tal vez uno de los más antiguos del que se tiene noción data de hace aproximadamente 30,000 años, del paleolítico superior y consiste en unas representaciones pictóricas en las que los antiguos registraron el número de días entre una Luna nueva y la siguiente (Durham, F. & Purrington, R. D, 1989) (v. también http://www.iac.es/project/arqueoastronomia/).
Esta protoastronomía subrayaba un aspecto de lo que llegaría a ser la ciencia: el aspecto computacional, el estudio de las regularidades. Con el tiempo, la observación astronómica fue progresando notablemente, siempre en la búsqueda de una mayor precisión, en la predicción en un principio, y en la medición en nuestros días.
Se cree que la Astronomía como ciencia surge en el siglo IV a. C. Aparece en Grecia una vez consolidado el desarrollo de la Geometría y, precisamente, como una necesidad que los griegos tuvieron de explicarse el movimiento de los planetas, ya que hasta entonces se creía que éstos se desplazaban en círculos geocéntricos.
Así pues, la Astronomía (del giego astron, astro y nomos, ley) es probablemente la más antigua de las ciencias y tiene por objeto el estudio de los astros, la determinación de su posición, así como la de sus movimientos, las causas que los originan y las propiedades físicas y químicas de los mismos.
Una vez que los astrónomos se dieron a la tarea de observar y estudiar formalmente y desde un marco científico a las estrellas, se empezaron a distinguir algunas ramas en esta ciencia. De ellas, la Astronomía estelar constituye la rama más antigua de la Astronomía; su objetivo principal es saber de qué manera están distribuidas las estrellas en el espacio, y cómo es que se agrupan para formar galaxias, cúmulos, etc.
La Astrofísica como ciencia surge con la invención del telescopio, durante el siglo XVII, pero sólo desde principos del siglo XX se la considera como una rama de la Astronomía. La Astrofísica acepta sin preguntas la localización y movimientos de los cuerpos celestes; se cuestiona, por ejemplo, de qué están compuestos cualquiera de estos cuerpos celestes, qué mantiene su luminosidad, cuán densos, calientes o masivos son, de dónde viene la energía que liberan, cómo nacen, se desarrollan y finalmente se extinguen o explotan, etc.
Actualmente la Astrofísica es la rama más importante de la Astronomía y ha contribuido grandemente al desarrollo de la Física, ciencia de la que a su vez ha tenido que echar mano para poder dar solución a los problemas con los que se encuentra.
¿Conoces alguna otra rama de la Astrofísica? ¿Sabes en qué se distinge la Astronomía de la Astrología?
http://www.astronomynotes.com/chapter1/s3.htm
Astronomía y Astrofísica.
Desde tiempos inmemoriales, el hombre se ha ocupado de la contemplación del cielo nocturno. Sabemos de esto gracias al estudio de un gran número de elementos (pinturas rupestres, estelas, códices, escritos, grabados, catálogos, etc.) en los que nuestros antepasados registraron sus conocimientos y que han llegado hasta nuestros días. De entre estos elementos, tal vez uno de los más antiguos del que se tiene noción data de hace aproximadamente 30,000 años, del paleolítico superior y consiste en unas representaciones pictóricas en las que los antiguos registraron el número de días entre una Luna nueva y la siguiente (Durham, F. & Purrington, R. D, 1989) (v. también http://www.iac.es/project/arqueoastronomia/).
Esta protoastronomía subrayaba un aspecto de lo que llegaría a ser la ciencia: el aspecto computacional, el estudio de las regularidades. Con el tiempo, la observación astronómica fue progresando notablemente, siempre en la búsqueda de una mayor precisión, en la predicción en un principio, y en la medición en nuestros días.
Se cree que la Astronomía como ciencia surge en el siglo IV a. C. Aparece en Grecia una vez consolidado el desarrollo de la Geometría y, precisamente, como una necesidad que los griegos tuvieron de explicarse el movimiento de los planetas, ya que hasta entonces se creía que éstos se desplazaban en círculos geocéntricos.
Así pues, la Astronomía (del giego astron, astro y nomos, ley) es probablemente la más antigua de las ciencias y tiene por objeto el estudio de los astros, la determinación de su posición, así como la de sus movimientos, las causas que los originan y las propiedades físicas y químicas de los mismos.
Una vez que los astrónomos se dieron a la tarea de observar y estudiar formalmente y desde un marco científico a las estrellas, se empezaron a distinguir algunas ramas en esta ciencia. De ellas, la Astronomía estelar constituye la rama más antigua de la Astronomía; su objetivo principal es saber de qué manera están distribuidas las estrellas en el espacio, y cómo es que se agrupan para formar galaxias, cúmulos, etc.
La Astrofísica como ciencia surge con la invención del telescopio, durante el siglo XVII, pero sólo desde principos del siglo XX se la considera como una rama de la Astronomía. La Astrofísica acepta sin preguntas la localización y movimientos de los cuerpos celestes; se cuestiona, por ejemplo, de qué están compuestos cualquiera de estos cuerpos celestes, qué mantiene su luminosidad, cuán densos, calientes o masivos son, de dónde viene la energía que liberan, cómo nacen, se desarrollan y finalmente se extinguen o explotan, etc.
Actualmente la Astrofísica es la rama más importante de la Astronomía y ha contribuido grandemente al desarrollo de la Física, ciencia de la que a su vez ha tenido que echar mano para poder dar solución a los problemas con los que se encuentra.
¿Conoces alguna otra rama de la Astrofísica? ¿Sabes en qué se distinge la Astronomía de la Astrología?
sábado, 5 de septiembre de 2009
TABLA ESCALAS DEL UNIVERSO Y TAREA SOBRE LA "NEBULOSA DEL CANGREJO"
Chicos, aquí les dejo la tabla construida a propósito de la tarea "Escalas del Universo". Fue realizada por una de las compañeras del grupo. Espero sirva para socializar sus resultados.
Saludos!
En relación con la tarea sobre los remanentes de supernova, pueden dejar en esta entrada sus comentarios. Les dejo el vínculo que Manuel nos comparte.... chéquenlo!
Les dejo también este video sobre Betelgeuse (alfa orionis)...
Recuerden que el mecanismo para registrar su tarea es participar con sus comentarios en esta entrada.
Nos escribimos!
viernes, 4 de septiembre de 2009
La paralaje
Introducción a la Astrofísica
Actividad práctica α: Paralaje
Propósito:
Que los estudiantes “exploren” el concepto de PARALAJE, una técnica fundamental para la medición de distancias estelares.
Materiales:
•Cinta métrica
Antecedentes y teoría:
Uno de los problemas más difíciles en la Astronomía es la determinación de distancias a objetos celestes. Existen cuatro métodos básicos de determinación de distancias: radar, paralaje, estándares lumínicos y la ley de Hubble. Cada uno de estos métodos es más útil a ciertas distancias: mientras que el radar es útil para los objetos más cercanos (por ejemplo, la Luna), la ley de Hubble es útil a escalas de distancia mayores. En este ejercicio, investigaremos el uso de la paralaje para determinar distancias.
Aunque sean observadas con los telescopios más grandes, las estrellas siguen siendo puntos de luz. A pesar de que podamos decir mucho acerca de una estrella a través de su luz, estas observaciones no nos brindan una escala de referencia que podamos utilizar para determinar su distancia. Para ello, necesitamos hacer uso de un método con el cual ya te encuentras familiarizado: la paralaje.
La paralaje es un método puramente geométrico que depende de la distancia a la estrella, el tamaño de la órbita de la Tierra y la medición precisa del movimiento de la estrella bajo estudio relativo a las distantes estrellas de fondo que se encuentran casi fijas durante el curso de 6 meses.
Actividad práctica α: Paralaje
Propósito:
Que los estudiantes “exploren” el concepto de PARALAJE, una técnica fundamental para la medición de distancias estelares.
Materiales:
•Cinta métrica
Antecedentes y teoría:
Uno de los problemas más difíciles en la Astronomía es la determinación de distancias a objetos celestes. Existen cuatro métodos básicos de determinación de distancias: radar, paralaje, estándares lumínicos y la ley de Hubble. Cada uno de estos métodos es más útil a ciertas distancias: mientras que el radar es útil para los objetos más cercanos (por ejemplo, la Luna), la ley de Hubble es útil a escalas de distancia mayores. En este ejercicio, investigaremos el uso de la paralaje para determinar distancias.
Aunque sean observadas con los telescopios más grandes, las estrellas siguen siendo puntos de luz. A pesar de que podamos decir mucho acerca de una estrella a través de su luz, estas observaciones no nos brindan una escala de referencia que podamos utilizar para determinar su distancia. Para ello, necesitamos hacer uso de un método con el cual ya te encuentras familiarizado: la paralaje.
La paralaje es un método puramente geométrico que depende de la distancia a la estrella, el tamaño de la órbita de la Tierra y la medición precisa del movimiento de la estrella bajo estudio relativo a las distantes estrellas de fondo que se encuentran casi fijas durante el curso de 6 meses.
Fig. 1. La paralaje de una estrellaSi podemos determinar el ángulo p a una estrella próxima a partir de su movimiento aparente en el cielo al paso de 6 meses, dado que sabemos que la distancia Tierra-Sol es 1AU, podemos determinar la distancia a la estrella.
Definición: El ángulo p subtendido por la distancia Tierra-Sol (1 AU) es de 1 segundo de arco (=1°/3600) si la distancia al objeto es de 1 parsec.
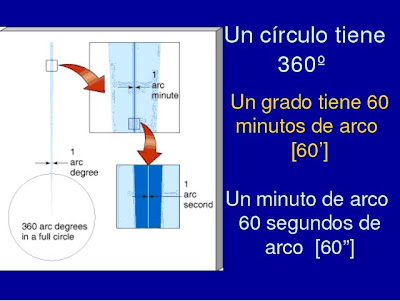
La estrella, el Sol y la Tierra forman un triángulo rectángulo a partir del cual, si el ángulo p y el cateto opuesto es conocido, el cateto adyacente puede ser calculado. Por trigonometría, tenemos:
Si p=1°/3600, entonces d = ___________ AU = 1 parsec = 3.26 años luz. El grupo estelar más cercano se encuentra a una distancia mayor que 1 parsec, lo que quiere decir que todas las estrellas tienen paralajes menores que 1 segundo de arco.Paralaje en el AULA
Una buena forma de ilustrar el cálculo de distancias paralácticas es utilizando un objeto sostenido con el brazo extendido directamente al frente de nuestros ojos. Para esta actividad, sostendrás un lápiz o un bolígrafo con tu brazo extendido y medirás la paralaje del objeto.
1. Un miembro del grupo se colocará a una distancia de aproximadamente 15 pies del pizarrón o de alguna pared.
2. Ese miembro del grupo sostendrá un lápiz verticalmente con su brazo extendido.
3. Otro miembro del grupo medirá la distancia desde el lápiz hasta la frente, teniendo cuidado de resguardar sus ojos. L = ___ cm.
4. Quien sostiene el lápiz se cubrirá un ojo y pedirá a otro miembro del grupo que trace una línea vertical en el pizarrón que esté alineada en correspondencia con el lápiz.
5. Ahora se cubrirá el otro ojo y pedirá que marquen una segunda línea vertical. Podremos percibir que el lápiz parece cambiar de posición relativa al pizarrón debido a que estamos cambiando el punto de observación de un ojo al otro.
6. Cuidadosamente, midan la distancia ojo-ojo. E = ___ cm
7. Cada miembro del grupo sostendrá el lápiz, alineará su ojo derecho con la marca de la izquierda en el pizarrón y repetirá el mismo procedimiento con el otro ojo. ¿Se alinea el lápiz con la marca de la derecha en el pizarrón? Explica.
2. Ese miembro del grupo sostendrá un lápiz verticalmente con su brazo extendido.
3. Otro miembro del grupo medirá la distancia desde el lápiz hasta la frente, teniendo cuidado de resguardar sus ojos. L = ___ cm.
4. Quien sostiene el lápiz se cubrirá un ojo y pedirá a otro miembro del grupo que trace una línea vertical en el pizarrón que esté alineada en correspondencia con el lápiz.
5. Ahora se cubrirá el otro ojo y pedirá que marquen una segunda línea vertical. Podremos percibir que el lápiz parece cambiar de posición relativa al pizarrón debido a que estamos cambiando el punto de observación de un ojo al otro.
6. Cuidadosamente, midan la distancia ojo-ojo. E = ___ cm
7. Cada miembro del grupo sostendrá el lápiz, alineará su ojo derecho con la marca de la izquierda en el pizarrón y repetirá el mismo procedimiento con el otro ojo. ¿Se alinea el lápiz con la marca de la derecha en el pizarrón? Explica.
Calculen el desplazamiento angular del lápiz. Este es la paralaje del lápiz. Ese ángulo (α en la figura inferior) será el mismo ángulo que el formado por los ojos del observador y el lápiz (ver figuras inferiores). Por convención, para la paralaje se acostumbra determinar la mitad del ángulo: α/2.
Fig. 2. Vista superior del ejercicio “Paralaje en el AULA”.
Fig. 3. Vista amplificada de una región de la figura anterior.Para el triángulo sombreado, tenemos:
Utilizando esta fórmula y tus medidas de E (espaciamiento entre los ojos) y L (longitud del brazo), calcula el ángulo paraláctico α/2 (la mitad del ángulo subtendido por los ojos o por las marcas).
tan(α/2) = ___ ------> α/2 = ___ degrees.
Si conocemos este ángulo y la distancia de ojo a ojo E pero no la longitud del brazo, podemos calcular la distancia del ojo al lápiz L utilizando la fórmula anterior. Para estrellas reales en lugar de lápices, si conocemos la distancia entre lugares en la órbita de la Tierra y el ángulo que una estrella describe relativo a las estrellas distantes, entonces utilizamos la fórmula obtenida previamente para calcular la distancia a la estrella.
Conocemos el espacio angular de las estrellas distantes debido a su RA y DEC. Si percibimos movimiento de las estrellas cercanas relativo a las estrellas distantes durante un periodo de 6 meses, podemos determinar la distancia angular que se desplaza una estrella cercana. Entonces tenemos el ángulo, y conocemos un lado del triángulo (distancia Tierra-Sol), de modo que podemos resolver para la distancia a la estrella.
Paralaje simulado:
Este diagrama muestra cómo una estrella cercana cambia su posición relativa a las estrellas de fondo debido al movimiento de la Tierra.
Una vez que hayas comprendido en qué consiste el cálculo de la paralaje estelar, visita el siguiente sitio:
1. Familiarízate con la animación.
2. La línea de visión de la Tierra a la estrella cercana cambia con relación a las estrellas más distantes. Esto es, las estrellas cercanas parecen moverse con relación a las estrellas más distantes que no muestrean movimiento aparente perceptible. Como sabemos la separación angular entre las estrellas distantes, podemos medir el movimiento angular aparente de las estrellas cercanas. Este es la paralaje de la estrella. Intenta describir con tus palabras el movimiento que percibirías como observador desde la estrella y desde la Tierra.
3. Describe lo que ocurriría si la estrella se alejara del Sol lo más lejos posible ¿cómo cambia el movimiento visto desde la Tierra?
4. En el cálculo de la paralaje realizado en el AULA, utilizamos nuestros ojos para cambiar la posición de visión. ¿Qué cambios ocurrirán en nuestra posición de visión en el caso de observaciones de la paralaje estelar?
5. Imagina ahora que la estrella se encuentra lo más cerca del Sol posible. Describe cómo es la paralaje que podría medirse en relación con la que se obtendría en 3.
2. La línea de visión de la Tierra a la estrella cercana cambia con relación a las estrellas más distantes. Esto es, las estrellas cercanas parecen moverse con relación a las estrellas más distantes que no muestrean movimiento aparente perceptible. Como sabemos la separación angular entre las estrellas distantes, podemos medir el movimiento angular aparente de las estrellas cercanas. Este es la paralaje de la estrella. Intenta describir con tus palabras el movimiento que percibirías como observador desde la estrella y desde la Tierra.
3. Describe lo que ocurriría si la estrella se alejara del Sol lo más lejos posible ¿cómo cambia el movimiento visto desde la Tierra?
4. En el cálculo de la paralaje realizado en el AULA, utilizamos nuestros ojos para cambiar la posición de visión. ¿Qué cambios ocurrirán en nuestra posición de visión en el caso de observaciones de la paralaje estelar?
5. Imagina ahora que la estrella se encuentra lo más cerca del Sol posible. Describe cómo es la paralaje que podría medirse en relación con la que se obtendría en 3.
CONTESTA LAS SIGUIENTES PREGUNTAS (no olvides hacer evidente la fuente de información):
1. ¿A qué estrella se le ha determinado el mayor ángulo paraláctico?
2. ¿Cuál es el límite para la determinación de distancias utilizando esta técnica?
3. ¿Podríamos obtener mejores resultados utilizando la técnica de la paralaje desde Marte?
Direcciones electrónicas de sitios tomados como referencia para el diseño de la actividad:
Les invito a adjuntar sus comentarios y resultados en relación con la práctica; asimismo, les recuerdo que la fecha límite para realizar esta actividad es el próximo martes 8 de septiembre a las 16:30.
Los comentarios deben realizarse de manera individual, tomando como guía los puntos 2,3,4 y 5 de la sección "paralaje simulado", así como las respuestas a las tres preguntas del final de la entrada.
lunes, 31 de agosto de 2009
Aproximaciones en las ecuaciones de la Astrofísica
Objetivos:
Que el estudiante comprenda la manera en que las aproximaciones de primer orden se utilizan en el estudio de los objetos astrofísicos.
Contenido:
Aproximaciones de primer orden
Estimación del orden de magnitud.
Relaciones de proporcionalidad.
Análisis dimensional.
Los objetos astrofísicos, ya sean planetas, estrellas, nebulosas o galaxias, son sistemas muy complejos. Con objeto de simplificar los sistemas de ecuaciones que describen a estos objetos hasta en punto en que pueda dárseles solución, los astrofísicos utilizan aproximaciones a las funciones involucradas. Las aproximaciones utilizadas algunas veces en astrofísica pueden parecer, en un primer momento, muy burdas, sin embargo, como comprobaremos en esta actividad, permiten visualizar de manera general las características de los sistemas astrofísicos.
La expansión en serie de potencias es una herramienta muy útil para obtener buenas aproximaciones simples. Al realizar esta tarea de aprendizaje utilizarás esta herramienta matemática y comprenderás, a partir del estudio de casos, la manera en que las aproximaciones son utilizadas en la astrofísica para simplificar la resolución de las ecuaciones involucradas en la descripción de los fenómenos. De manera particular, en esta tarea utilizaremos las aproximaciones para hacer soluble una ecuación diferencial que describe el movimiento de una estrella en una galaxia.
RELACIONES DE PROPORCIONALIDAD.
Algunas veces, la diferencia entre resultados obtenidos a partir de distintas aproximaciones o suposiciones toma la forma de una función común de algún parámetro físico fundamental multiplicada por distintos factores que son independientes de estos parámetros. Como ejemplificamos en clase, en estos casos, podemos utilizar las relaciones de proporcionalidad para contar con una perspectiva global que nos permita aproximarnos de manera general a la comprensión de un fenómeno en particular.
ANÁLISIS DIMENSIONAL.
Esta herramienta es igualmente útil para poder predecir en una primera aproximación tamaños de objetos o escalas de tiempo.
Que el estudiante comprenda la manera en que las aproximaciones de primer orden se utilizan en el estudio de los objetos astrofísicos.
Contenido:
Aproximaciones de primer orden
Estimación del orden de magnitud.
Relaciones de proporcionalidad.
Análisis dimensional.
Los objetos astrofísicos, ya sean planetas, estrellas, nebulosas o galaxias, son sistemas muy complejos. Con objeto de simplificar los sistemas de ecuaciones que describen a estos objetos hasta en punto en que pueda dárseles solución, los astrofísicos utilizan aproximaciones a las funciones involucradas. Las aproximaciones utilizadas algunas veces en astrofísica pueden parecer, en un primer momento, muy burdas, sin embargo, como comprobaremos en esta actividad, permiten visualizar de manera general las características de los sistemas astrofísicos.
La expansión en serie de potencias es una herramienta muy útil para obtener buenas aproximaciones simples. Al realizar esta tarea de aprendizaje utilizarás esta herramienta matemática y comprenderás, a partir del estudio de casos, la manera en que las aproximaciones son utilizadas en la astrofísica para simplificar la resolución de las ecuaciones involucradas en la descripción de los fenómenos. De manera particular, en esta tarea utilizaremos las aproximaciones para hacer soluble una ecuación diferencial que describe el movimiento de una estrella en una galaxia.
RELACIONES DE PROPORCIONALIDAD.
Algunas veces, la diferencia entre resultados obtenidos a partir de distintas aproximaciones o suposiciones toma la forma de una función común de algún parámetro físico fundamental multiplicada por distintos factores que son independientes de estos parámetros. Como ejemplificamos en clase, en estos casos, podemos utilizar las relaciones de proporcionalidad para contar con una perspectiva global que nos permita aproximarnos de manera general a la comprensión de un fenómeno en particular.
ANÁLISIS DIMENSIONAL.
Esta herramienta es igualmente útil para poder predecir en una primera aproximación tamaños de objetos o escalas de tiempo.
jueves, 20 de agosto de 2009
La escala del Universo.
(Imagen tomada de www.astromia.com/fotostierra/tierrayluna.htm
)
El video que analizamos ha logrado empezar a integrar nuestro equipo de trabajo. Ha motivado la expresión de nuestras perspectivas acerca de la vastedad del Universo... ¿Creen que realmente podamos comprender qué TAN GRANDE es?. Powers of ten, un clásico de Charles y Ray Eames, nos permite viajar por todas esas potencias de diez que hay que tomar en cuenta para incluir todos los aspectos estudiados por la Astronomía contemporánea.
Debido a las inmensas distancias involucradas, y al amplio rango de escalas que utilizaremos en nuestro curso (desde la atómica, pasando por la humana, hasta los alcances del Universo Astronómico) es importante comprender y alcanzar el dominio de las potencias de diez, la notación científica y los órdenes de Magnitud.
Las potencias de diez se refieren a la secuencia de números formada tomando la base 10 a diferentes potencias enteras, por ejemplo 1, 10, 100, 1000, ..., lo mismo que 1.1, 0.01, 0.001, etc.
En la notación científica se especifican abreviadamente las potencias de diez implícitas en un número en particular.
La idea detrás de los órdenes de magnitud es la siguiente: 1 orden de magnitud significa un factor de 10 (de modo que 2 órdenes de magnitud es igual a 100, etc.). Así, los números 0.003 y 30 están separados por 4 órdenes de magnitud, o 10000. Es más fácil visualizar esto escribiendo los números en notación científica, 0.003=3x10^-3 y 30=3x10^1, y notando que la diferencia en los exponentes 1 menos -3 es 4.
)El video que analizamos ha logrado empezar a integrar nuestro equipo de trabajo. Ha motivado la expresión de nuestras perspectivas acerca de la vastedad del Universo... ¿Creen que realmente podamos comprender qué TAN GRANDE es?. Powers of ten, un clásico de Charles y Ray Eames, nos permite viajar por todas esas potencias de diez que hay que tomar en cuenta para incluir todos los aspectos estudiados por la Astronomía contemporánea.
Debido a las inmensas distancias involucradas, y al amplio rango de escalas que utilizaremos en nuestro curso (desde la atómica, pasando por la humana, hasta los alcances del Universo Astronómico) es importante comprender y alcanzar el dominio de las potencias de diez, la notación científica y los órdenes de Magnitud.
Las potencias de diez se refieren a la secuencia de números formada tomando la base 10 a diferentes potencias enteras, por ejemplo 1, 10, 100, 1000, ..., lo mismo que 1.1, 0.01, 0.001, etc.
En la notación científica se especifican abreviadamente las potencias de diez implícitas en un número en particular.
La idea detrás de los órdenes de magnitud es la siguiente: 1 orden de magnitud significa un factor de 10 (de modo que 2 órdenes de magnitud es igual a 100, etc.). Así, los números 0.003 y 30 están separados por 4 órdenes de magnitud, o 10000. Es más fácil visualizar esto escribiendo los números en notación científica, 0.003=3x10^-3 y 30=3x10^1, y notando que la diferencia en los exponentes 1 menos -3 es 4.
Como las cantidades en Astronomía, tales como distancias, masas o luminosidades cubren un espectro muy amplio, es útil desarrollar la habilidad para hacer estimaciones y aproximar los valores al orden de magntud más cercano. Este tipo de cálculo abreviado recibe el nombre de estimación del orden de magnitud.
¡ATENCIÓN! Orden de magnitud no es lo mismo que magnitud (de una estrella, por ejemplo) la cual denota brillantez. Regresaremos a este punto cuando estudiemos el brillo estelar. Así que recuerden que cuando digamos "orden de magnitud" nos referiremos a factores de 10 y que cuando digamos "magnitud" nos referiremos a las unidades de brillo relativo.
Para ayudarnos a visualizar las escalas del Universo, tomemos como referencia la "Escala Manual del Universo" propuesta de Steven T. Myers, plasmada en su curso "Survey of the Universe" (disponible en línea en http://www.aoc.nrao.edu/~smyers/courses/astro01/L1.html#sec.2) y que se basa en el tamaño de su puño (del tuyo en este caso). En promedio, el puño de una persona que comprime una pelota mide 10 cm. Hagamos que esto represente a la Tierra. Sabemos que el radio ecuatorial de la Tierra es de 6378 km, lo que significa que tiene un diámetro de alrededor de 12800 km (redondeado, en un intento por hacer los cálculos más sencillos). La Luna tiene un radio de 1738 km (un diámetro de aproximadamente 3500 km), o 27% el diámetro de la Tierra. Esto hace 2.7 centímetros en nuestra escala, o aproximadamente el tamaño de un pulgar. La Luna se encuentra a 384000 km de la Tierra, o visto de otra forma, a 30 diámetros terrestres (=384000/12800). Entonces, para representar a la Tierra y su satélite natural en nuestra escala, debemos colocar a la Luna (el pulgar) a 30x(10cm)=300cm=3m de nuestro puño. Trata de vivenciar esta representación pidiendo a un(a) compañer@ que represente a la Luna con su pulgar ubicado a 3m de tu puño (la Tierra) e imaginen a la nave espacial Apolo (que en nuestra escala medirá aproximadamente 0.002 mm o 2 micras, ¡un grano de polvo!) siendo lanzada desde tu puño para cruzar los tres metros que la separan del pulgar de tu compañer@.
¡ATENCIÓN! Orden de magnitud no es lo mismo que magnitud (de una estrella, por ejemplo) la cual denota brillantez. Regresaremos a este punto cuando estudiemos el brillo estelar. Así que recuerden que cuando digamos "orden de magnitud" nos referiremos a factores de 10 y que cuando digamos "magnitud" nos referiremos a las unidades de brillo relativo.
Para ayudarnos a visualizar las escalas del Universo, tomemos como referencia la "Escala Manual del Universo" propuesta de Steven T. Myers, plasmada en su curso "Survey of the Universe" (disponible en línea en http://www.aoc.nrao.edu/~smyers/courses/astro01/L1.html#sec.2) y que se basa en el tamaño de su puño (del tuyo en este caso). En promedio, el puño de una persona que comprime una pelota mide 10 cm. Hagamos que esto represente a la Tierra. Sabemos que el radio ecuatorial de la Tierra es de 6378 km, lo que significa que tiene un diámetro de alrededor de 12800 km (redondeado, en un intento por hacer los cálculos más sencillos). La Luna tiene un radio de 1738 km (un diámetro de aproximadamente 3500 km), o 27% el diámetro de la Tierra. Esto hace 2.7 centímetros en nuestra escala, o aproximadamente el tamaño de un pulgar. La Luna se encuentra a 384000 km de la Tierra, o visto de otra forma, a 30 diámetros terrestres (=384000/12800). Entonces, para representar a la Tierra y su satélite natural en nuestra escala, debemos colocar a la Luna (el pulgar) a 30x(10cm)=300cm=3m de nuestro puño. Trata de vivenciar esta representación pidiendo a un(a) compañer@ que represente a la Luna con su pulgar ubicado a 3m de tu puño (la Tierra) e imaginen a la nave espacial Apolo (que en nuestra escala medirá aproximadamente 0.002 mm o 2 micras, ¡un grano de polvo!) siendo lanzada desde tu puño para cruzar los tres metros que la separan del pulgar de tu compañer@.
El Sol tiene un diámetro aproximado de 1.4x10^6 km, ¿que diámetro tendrá en nuestra escala?. La distancia promedio entre el Sol y la Tierra es de 150x10^6 km. ¿A qué distancia de tu puño deberías colocarlo para ejemplificar su posición respecto a la Tierra?
La distancia promedio entre la Tierra y el Sol se conoce como Unidad Astronómica, o AU, por sus siglas en inglés. La Unidad Astronómica es una medida conveniente para medir las órbitas de los planetas en nuestro sistema solar. ¿A cuánto equivale 1 AU en nuestra escala?
Los invito a adjuntar sus respuestas.
martes, 18 de agosto de 2009
¿Qué tan grande es el universo?
Utilizaremos un modelo a escala del sistema solar y la Galaxia para tratar de dar respuesta a esta pregunta.
Chequen el video:
El original con audio en inglés...
Chequen el video:
El original con audio en inglés...
martes, 21 de julio de 2009
Metodología de trabajo
Para lograr los objetivos marcados en este programa, se requiere de la participación conjunta del profesor y los estudiantes, de manera que algunas veces la exposición de un tema estará a cargo del profesor y otras veces los estudiantes (ya sea de manera individual o por equipo) prepararán y expondrán algún tema en clase.
A lo largo de cada micro unidad de competencia cada estudiante realizará las distintas actividades que se encuentran marcadas en este programa (lecturas, resolución de problemas, realización de síntesis, ensayos e investigaciones, etc.), esto con la finalidad de promover por una parte el desarrollo de las habilidades necesarias que su formación como universitario y científico requiere y por la otra la participación activa en cada una de las clases.
Por su parte, a lo largo del curso evaluará los productos de cada actividad y retroalimentará a los estudiantes para que corrijan las fallas en que hayan incurrido.
A lo largo de cada micro unidad de competencia cada estudiante realizará las distintas actividades que se encuentran marcadas en este programa (lecturas, resolución de problemas, realización de síntesis, ensayos e investigaciones, etc.), esto con la finalidad de promover por una parte el desarrollo de las habilidades necesarias que su formación como universitario y científico requiere y por la otra la participación activa en cada una de las clases.
Por su parte, a lo largo del curso evaluará los productos de cada actividad y retroalimentará a los estudiantes para que corrijan las fallas en que hayan incurrido.
Introducción a la Astrofísica Agosto 09/Febrero 10 Prof. Argelia Sol-Haret Báez Barrios
La Astrofísica es una ciencia en la que se conjugan los esfuerzos de dos ciencias, la Astronomía y la Física, con el objetivo común de estudiar el Universo.
Siendo este un curso de Astrofísica, durante el semestre realizaremos un estudio general del Universo partiendo de las bases teóricas que nuestra formación como físicos nos ha proporcionado.
Resulta evidente que tratar de resumir al Universo en un curso semestral es labor de titanes, sin embargo, utilizando como estrategia recursiva aquella inspirada en la máxima "Divide et vinces" (divide y vencerás), con el fin de adentrarnos en el vasto mundo de la Astronomía, en este curso iremos conociendo poco a poco y de manera particular cada uno de los principales componentes del Universo, desde los que nos son más comunes –tales como los planetas, los cometas, las estrellas, la Vía Láctea- pasando por las agrupaciones de galaxias y llegando hasta los remotos cuásares y los enigmáticos agujeros negros.
Sin lugar a dudas, el conocimiento individual y la caracterización física de los distintos objetos que conforman el Universo nos permitirá entender cómo se interrelacionan entre si, discernir acerca del contexto dentro del cual han evolucionado, la manera en que están distribuidos, así como acercarnos al estudio de las leyes físicas que rigen su comportamiento tanto de manera particular como a nivel global.
IMPORTANCIA DE LA ASIGNATURA DENTRO DE LA FORMACIÓN PROFESIONAL
El cursar esta asignatura permite al alumno decidir su interés por la Física Aplicada, mediante el desarrollo de habilidades y técnicas de investigación científica en un campo determinado.
¿CÓMO CONTACTARME?
Argelia Sol-Haret Báez Barrios
solharet@gmail.com
arbaez@uv.mx
cel: 2281548840
Asesorías:
Viernes 14-16
¡No te quedes solo con las dudas!
Suscribirse a:
Comentarios (Atom)